Lab 11 - Simulator Localization
In this lab I used the FlatLand simulator to implement a Bayes Filter localization model on a simulated robot car. The car moves through a set trajectory provided by the professor, spinning in place at each waypoint to collect TOF sensor data for localization. This sensor data is then fused with odometry data to provide an estimation of the pose of the robot.
Code:
def compute_control(cur_pose, prev_pose): """ Given the current and previous odometry poses, this function extracts the control information based on the odometry motion model. Args: cur_pose ([Pose]): Current Pose prev_pose ([Pose]): Previous Pose Returns: [delta_rot_1]: Rotation 1 (degrees) [delta_trans]: Translation (meters) [delta_rot_2]: Rotation 2 (degrees) """ delta_x, delta_y = cur_pose[0]-prev_pose[0], cur_pose[1]-prev_pose[1] move_angle = np.arctan2(delta_y, delta_x) * 180 / np.pi delta_rot1 = mapper.normalize_angle(move_angle - prev_pose[2]) delta_trans = np.sqrt(delta_x**2 + delta_y**2) delta_rot2 = mapper.normalize_angle(cur_pose[2] - move_angle) return delta_rot1, delta_trans, delta_rot2 def odom_motion_model(cur_pose, prev_pose, u): """ Odometry Motion Model Args: cur_pose ([Pose]): Current Pose prev_pose ([Pose]): Previous Pose (rot1, trans, rot2) (float, float, float): A tuple with control data in the format format (rot1, trans, rot2) with units (degrees, meters, degrees) Returns: prob [float]: Probability p(x'|x, u) """ r_sigma = loc.odom_rot_sigma t_sigma = loc.odom_trans_sigma dr1, dt, dr2 = compute_control(cur_pose, prev_pose) dr1_prob = loc.gaussian(u[0], dr1, r_sigma) dt_prob = loc.gaussian(u[1], dt, t_sigma) dr2_prob = loc.gaussian(u[2], dr2, r_sigma) return dr1_prob * dt_prob * dr2_prob def prediction_step(cur_odom, prev_odom): """ Prediction step of the Bayes Filter. Update the probabilities in loc.bel_bar based on loc.bel from the previous time step and the odometry motion model. Args: cur_odom ([Pose]): Current Pose prev_odom ([Pose]): Previous Pose """ #loop x_t u = compute_control(cur_odom, prev_odom) for x_i, x_a in enumerate(loc.bel_bar): for y_i, y_a in enumerate(x_a): for th_i, b_t in enumerate(y_a): sum_probs = 0 #loop x_t-1 for x_ind, x_arr in enumerate(loc.bel): for y_ind, y_arr in enumerate(x_arr): for th_ind, b_t1 in enumerate(y_arr): if (b_t1 < 0.05): continue pose_t = mapper.from_map(x_i, y_i, th_i) pose_t1 = mapper.from_map(x_ind, y_ind, th_ind) prob_xt = odom_motion_model(pose_t1, pose_t, u) p = prob_xt * b_t1 sum_probs += p loc.bel_bar[x_i, y_i, th_i] = sum_probs def sensor_model(pose): """ This is the equivalent of p(z|x). Args: pose ([ndarray]): A Pose Returns: [ndarray]: Returns a 1D array of size 18 (=loc.OBS_PER_CELL) with the likelihoods of each individual sensor measurement """ views = mapper.get_views(pose[0],pose[1],pose[2]) # prob_array = loc.gaussian(loc.obs_range_data[:,0], views, loc.sensor_sigma) prob_array = np.zeros(18) for i, ob in enumerate(loc.obs_range_data[:,0]): # print("ob, views:", ob, views[i]) prob_array[i] = loc.gaussian(ob, views[i], loc.sensor_sigma) # print (prob_array[i]) return prob_array * 1e8 def update_step(): """ Update step of the Bayes Filter. Update the probabilities in loc.bel based on loc.bel_bar and the sensor model. """ for x_ind, x_arr in enumerate(loc.bel_bar): for y_ind, y_arr in enumerate(x_arr): for th_ind, bel_b in enumerate(y_arr): sensor_mod = sensor_model(np.array([x_ind, y_ind, th_ind])) loc.bel[x_ind, y_ind, th_ind] = np.prod(sensor_mod) * bel_b loc.bel = loc.bel / np.sum(loc.bel)
Above is all of the code I implemented for this lab. The functions prediction_step and update_step are called after each time step executed in the robot's preset trajectory. They use odometry and sensor data respectively to form a belief of the robot's state. The remaining functions are helpers used in the calculation of belief. More details below.
Prediction Step:
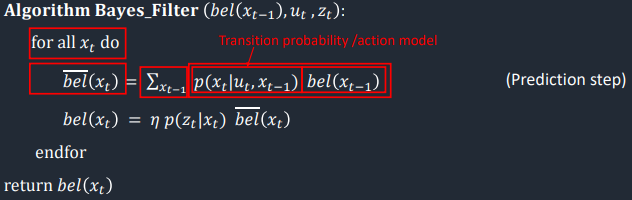
Here I fill the Localization class's bel_bar array with probabilities corresponding to how likely the robot is to be in a certain position given odometry data. The odometry data is obtained from the provided Commander class via the provided Trajectory class, and is a single pose representing the robot's belief of where it is based purely on it's initial position and control signals. This is similar to using the IMU or integrating the motor drive on a physical robot to estimate the position. These estimates are non-probabilistic and tend to quickly become inaccurate as errors accrue. The odometry for the robot's pose before and after moving is used to compute an estimate for the movement of the robot over the time step using the function compute_control. Then, this estimate is used in estimating the probability that the robot is currently in each possible state in the map. For each possible current pose, the code iterates over each possible previous pose and calculates the probability that it moved from the previous to current pose given the estimated odometry motion. This probability calculation is accomplished with the odom_motion_model function, which uses a gaussian distribution to model the motion. These probabilities are multiplied by the chance the robot was in the previous pose to begin with (taken from the Localization bel array), and summed for each current pose. This probability multiplication is an application of Bayes formula. This sum is stored in the Localization class's 3D bel_bar array, with the array index corresponding to the location of the of the current pose in the map in [x,y,theta] format. Thus the probability of the robot being in every pose in the map is calculated based on odometry and stored in bel_bar.
Update Step:

Next, sensor data is applied to the current pose probabilities in the bel_bar array to create a more informed estimate of the robot's probable current states. At every time step the robot turns 360 degrees while taking 18 TOF measurements. Then every state in bel_bar is cycled over, and the probability that the robot is in every possible state given those distance measurements is computed. This is done with the sensor_model helper function, which samples each observed distance measurements from a gaussian centered at pre-cached measurements expected for the pose in question. The probability of obtaining the observed measurements from the pose is taken as the product of these gaussian samples. Then Bayes formula is applied by multiplying the obtained probability for each state by the bel_bar pose probabilities to obtain more updated current pose probabilities. These are normalized and saved in the Localization class bel array. Note: In my implementation I was having underflow issues causing some loss of accuracy, so I multiplied all sensor_model values by 10^8. This factor helps in computation but is eliminated by normalization at the end.
Result:
Screen recording of localization in action:
Localization was accomplished in approximately two minutes without long delays between movements, so the time complexity of the Bayes Filter is decent.
Pose Plot (Red: odometry, Green: ground truth, Blue: belief)
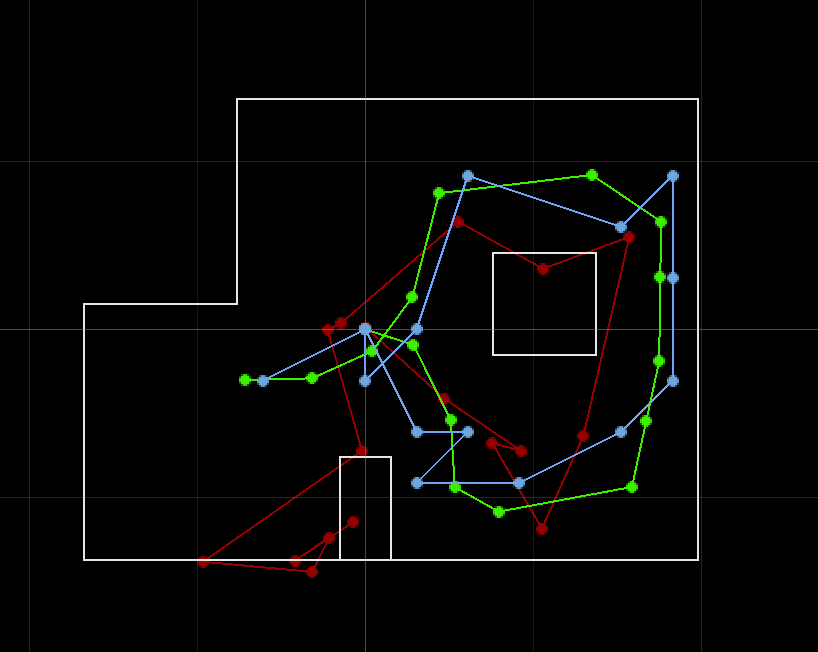
Success! The blue line (belief) follows the green line (ground truth) fairly closely, which implies that the Bayes filter was successful.