Lab 12 - Localization on Robot
In this lab I ran a limited Bayes Filter localization on the physical robot. At this point the robot is still not moving by itself around the map. Instead, I placed the robot in four marked locations on the map, had it take measurements while rotating, and ran the update step of the Bayes filter to estimate position based off of sensor data.
Simulated Localization:
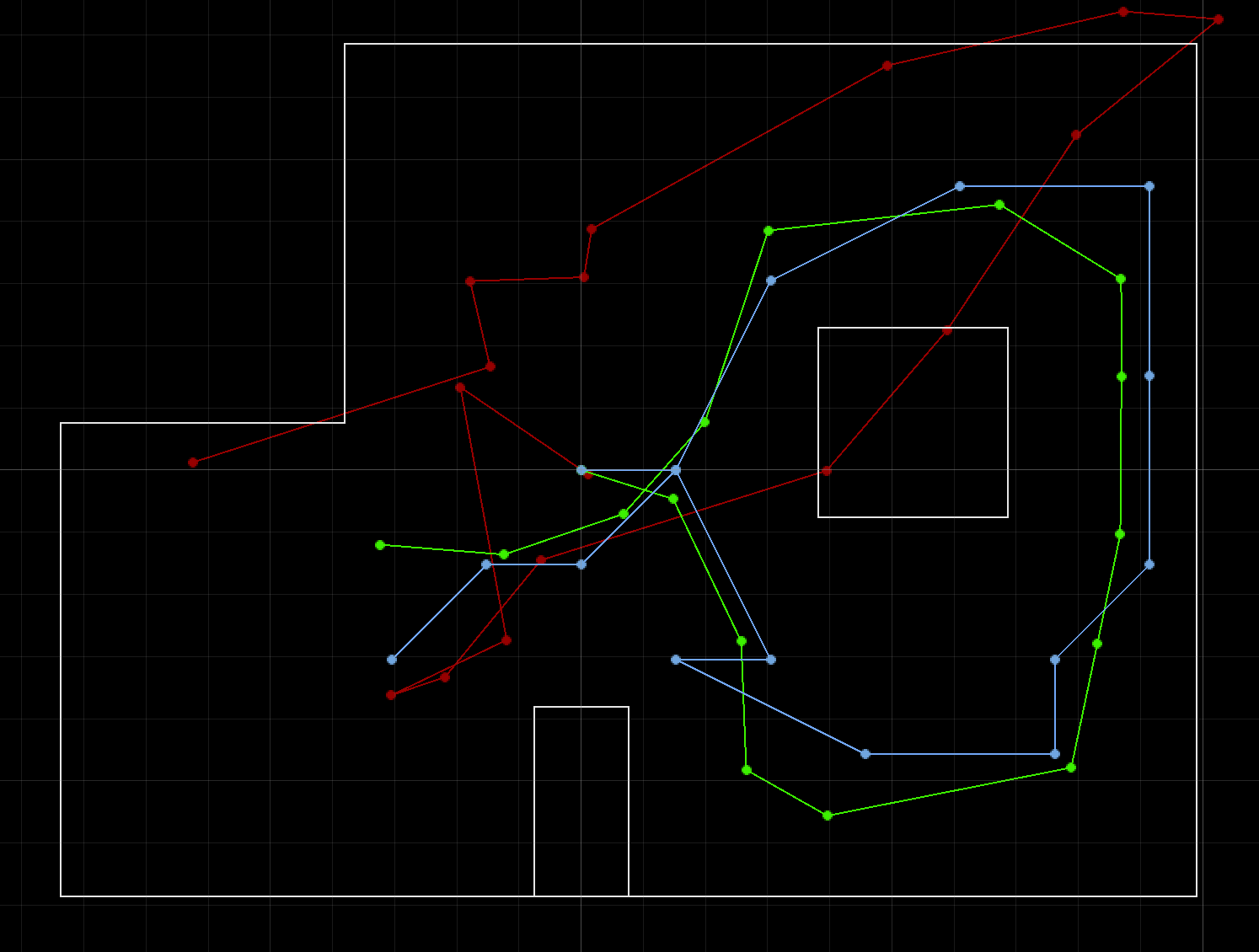
Before attempting localization on the robot, I ran the Bayes filter provided by course staff on the FlatLand simulator in order to assure there are no issues. Below is the plotter output from that run:
Simulated Localization Plot (Red: odometry, Green: ground truth, Blue: belief)
Observation Loop:
I used the same observation loop as in Lab 9, but adjusted the PID controller so that it would turn 20 degrees per observation rather than 24 degrees. Then I could collect 18 independent TOF observations instead of 15 readings like in Lab 9. The Python code used to collect and process the observation data is below:
Code to Perform Observation Loop
def perform_observation_loop(self, rot_vel=120): # Initialize my custom robot controller class rc = RobotControl(ble) # Spin in place with PWM = 95, collecting sensor data rc.spin_360(95) # We need to explicitly stop recording data after it stops spinning while rc.sensor_readings is None or len(rc.sensor_readings) <= 18: asyncio.run(asyncio.sleep(0.05)) rc.stop_recording() # Display the full sensor data cols = [ "time", "dist_r", "dist_f", "acc_x", "acc_y", "acc_z", "gyr_x", "gyr_y", "gyr_z", "mag_x", "mag_y", "mag_z", "temp" ] sensor_data = pd.DataFrame(rc.sensor_arr, columns=cols) # We only really care about the front ToF data though: sensor_ranges = (np.flip(sensor_data["dist_f"][:18].to_numpy()))[np.newaxis].T # Convert millimeters to meters sensor_ranges /= 1000 return sensor_ranges, sensor_ranges # We don't care about the second value
Localization:
This lab does not use the car's motors so odometry does not come into play. Therefore the prediction step is meaningless. I used exclusively the update step at each of four points to localize. This update step is identical to the one written in lab 11. Below are plots for the Belief given by the update step for each point:
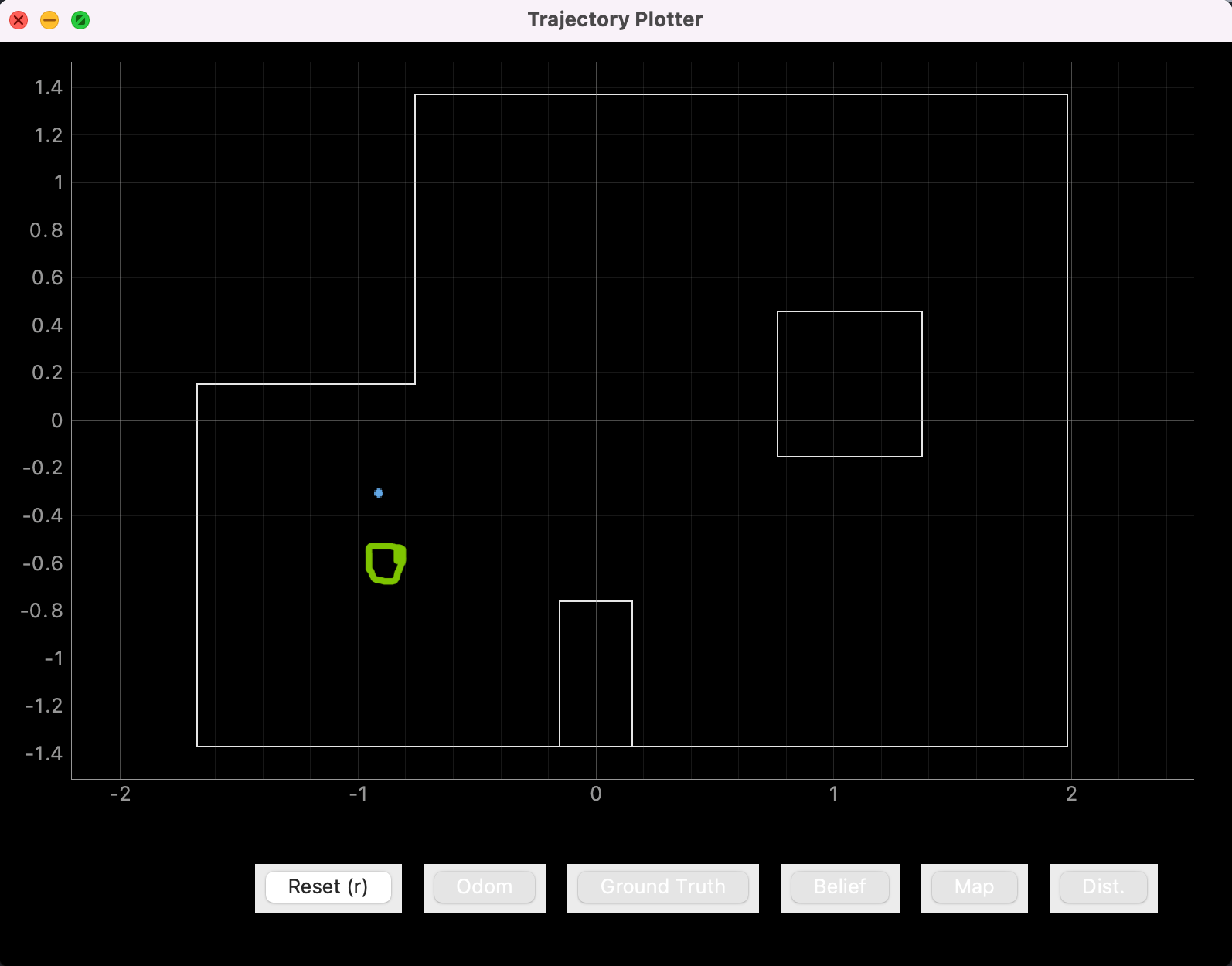
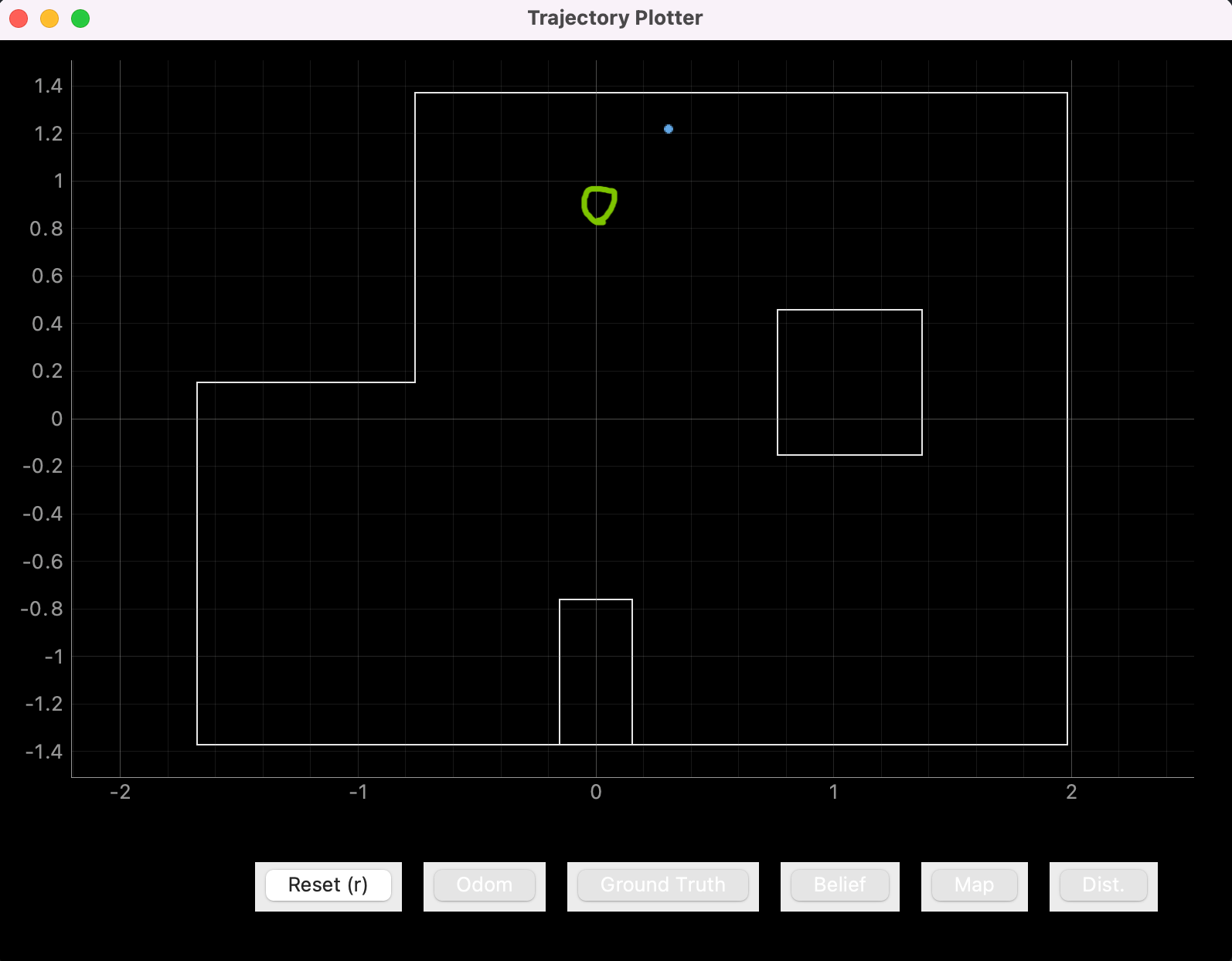
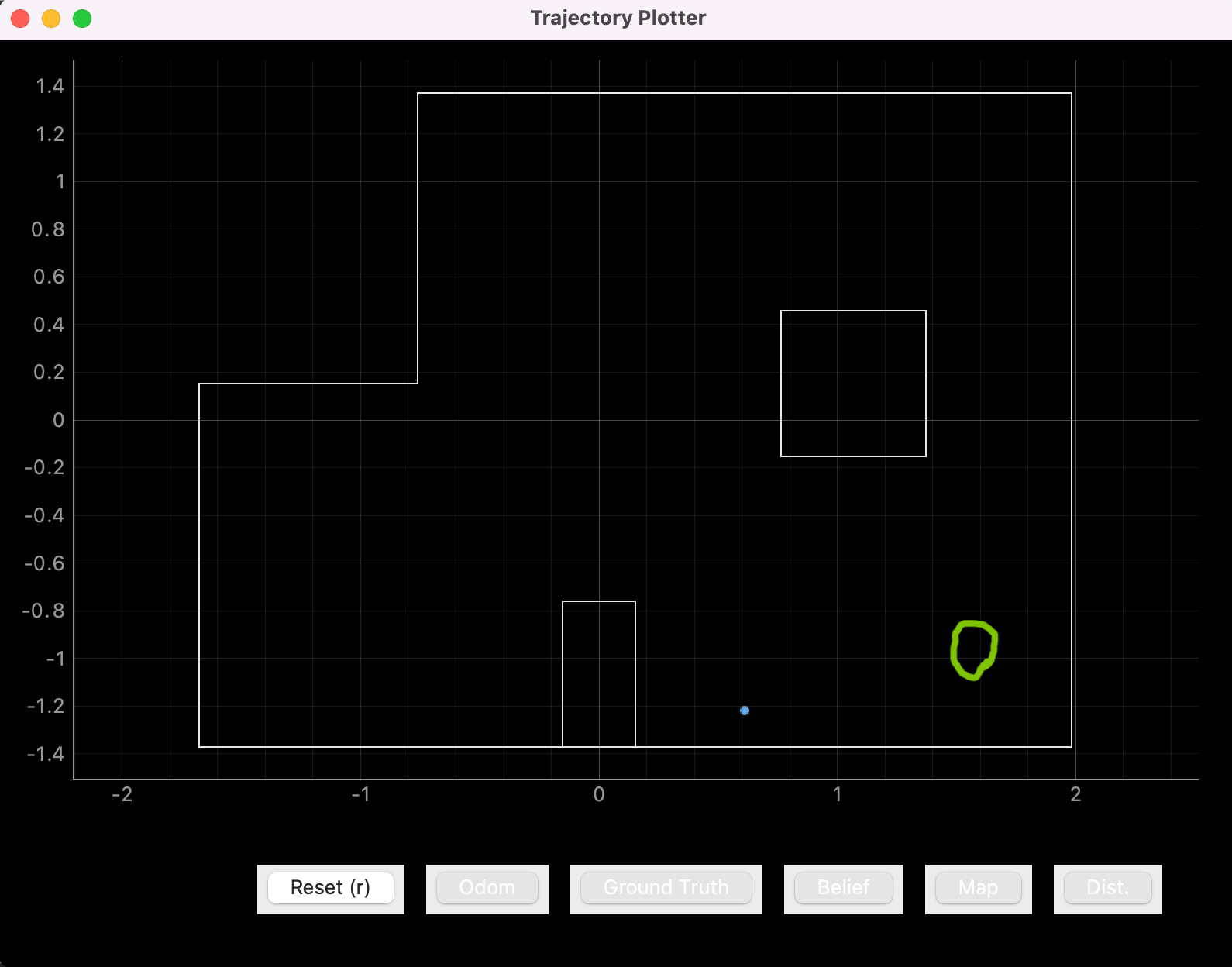
The blue dots represent the belief and the green circle surrounds the location the car was placed.
Point 1: (-3 ft, -2 ft, 0 deg)
Point 2: (0 ft ,3 ft, 0 deg)
Point 3: (5 ft, -3 ft, 0 deg)
Point 4: (5 ft, 3 ft, 0 deg)
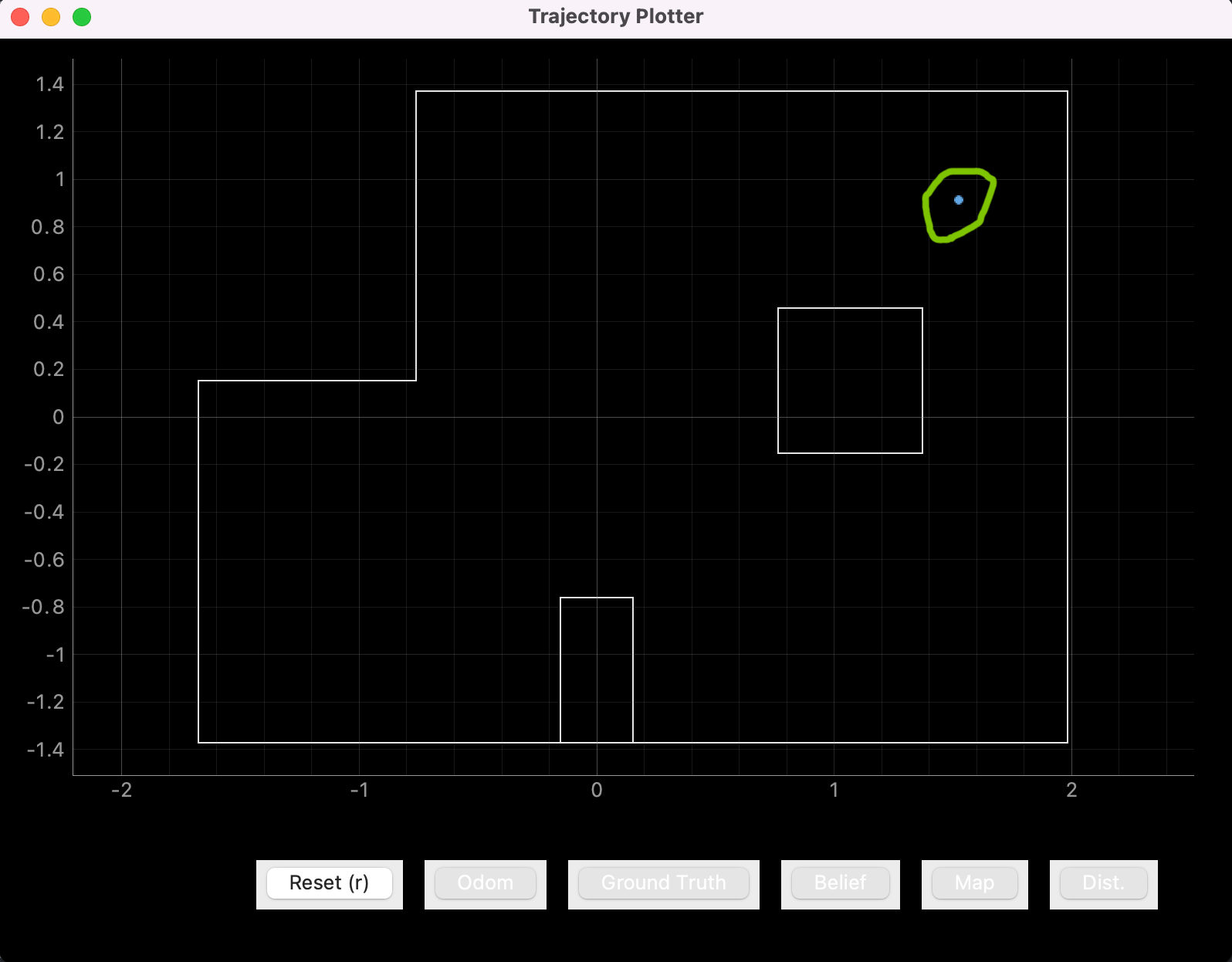
Orientation is not displayed in these plots but in each case it was near the correct value of zero degrees.
Conclusion:
In general localization was imperfect but came somewhat close. The exception is point 4, in which case localization was on the dot. The inaccuracies are likely due to error in the 20 degree rotations between observations and sensor noise.