Fast Robots

Lab 13 - Path Planning and Execution

The goal for this lab was to make the robot move through a set of waypoints using localization and control in real time. My approach was to loop through the waypoints and attempt to move directly from the car's current position towards the next waypoint using open loop control. The current pose of the car is established using Bayes filter localization.

Strategy:

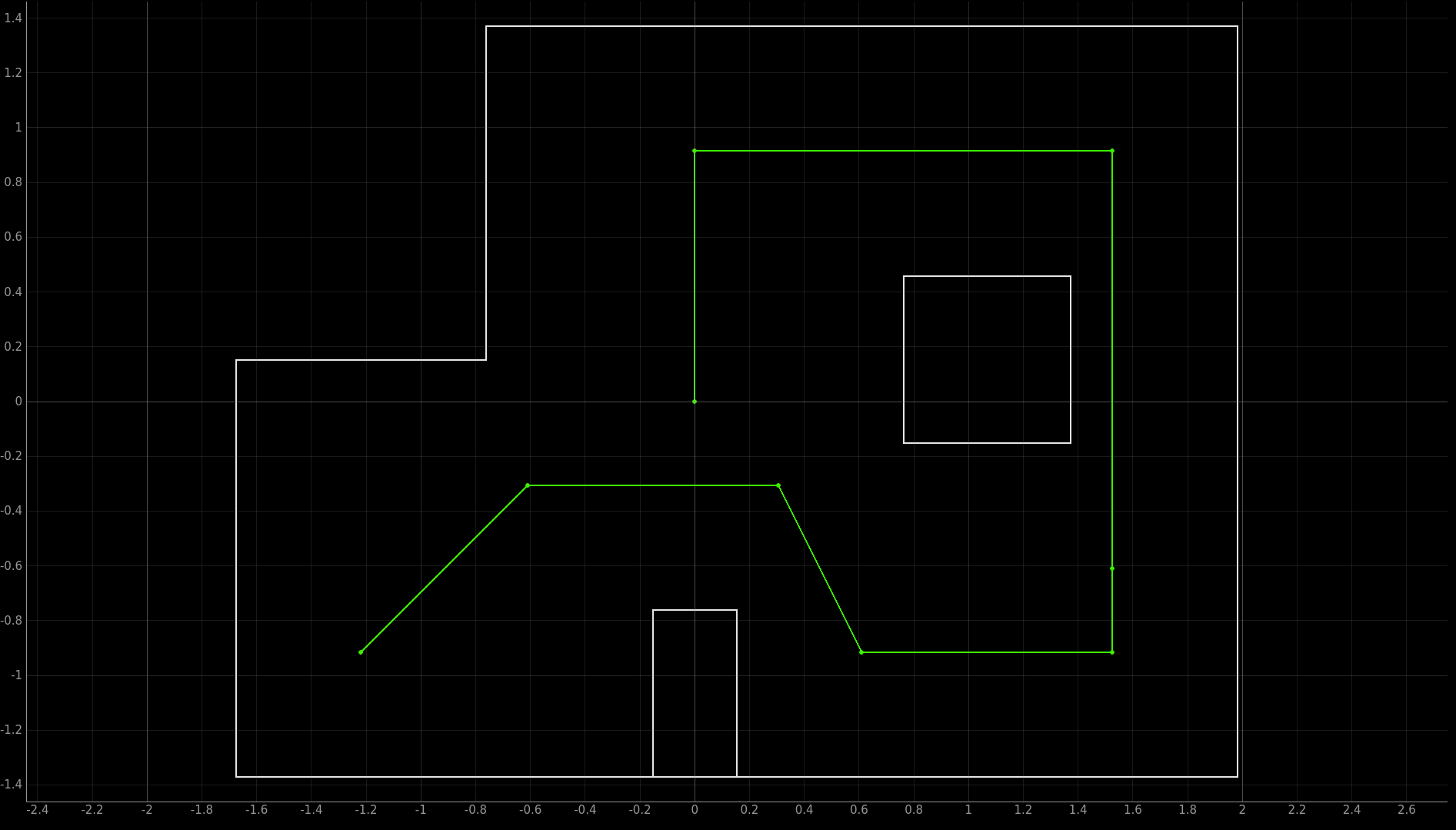
To successfully complete this lab the robot needed to move through the following waypoints, given in feet from the center of the map.

1. (-4, -3) start
2. (-2, -1)
3. (1, -1)
4. 4. (2, -3)
5. 5. (5, -3)
6. 6. (5, -2)
7. 7. (5, 3)
8. 8. (0, 3)
9. 9. (0, 0) end

Here is what that looks like on the map:

Waypoint Trajectory:

The logic used for moving from waypoint to waypoint is as follows. First, localization is executed to gather a pose estimate for the current state of the robot. If the robot is projected to be within one grid cell distance of the next waypoint then the next waypoint is incremented. If it is on the final waypoint then the control loop breaks and the robot does nothing. Otherwise, a rotation-translation-rotation control is formulated to move the robot from its current pose estimate to the next waypoint. This control is scaled to a motor PWM and duration command which is calibrated to match the degree and meter control outputs. Then when the motion command finishes, localization is run again and the cycle repeats. However, this only works if the robot encounters no obstacles while moving. If it encounters an obstacle, then a local obstacle avoidance planner takes over and uses right wall following until the obstacle is passed. At that point localization is run again and the cycle continues.

Code for Outer Logic:

# Run through each motion steps
i = 0
while True:
    
    ... Localization ...
    
    # Check if we reached a waypoint
    x, y, _ = argmax_bel[0]
    way_x = waypoints[i][0]
    way_y = waypoints[i][1]
    if way_x - 1 <= x <= way_x + 1 and way_y - 1 <= y <= way_y + 1:
        i += 1
        print(f"New goal waypoint {i}")
    
    # Termination condition
    if i == len(waypoints):
        break
    
    # Compute the necessary control to get to the next waypoint (assuming no obstacles)
    delta_rot_1, delta_trans, delta_rot_2 = loc.compute_control(waypoints_in_m[i], current_belief)
    speed_rot_1, time_rot_1 = rot_delta_to_pwm(delta_rot_1, boost)
    speed_trans, time_trans = trans_delta_to_pwm(delta_trans)
    speed_rot_2, time_rot_2 = rot_delta_to_pwm(delta_rot_2, boost)
    
    # Invoke motor inputs...
    # First rotation:
    if time_rot_1 < 0:
        rc.rotate_right(speed_rot_1)
    else:
        rc.rotate_left(speed_rot_1)
    await asyncio.sleep(abs(time_rot_1))
    rc.active_stop()
    
    await asyncio.sleep(1)
    
    # Try to move forward with the forward controls.
    # If there are obstacles, scrap the rest of the control and try again with new localization data.
    obstacles_avoided = execute_safe_trajectory(speed_trans, time_trans)
    if obstacles_avoided:
        continue
    
    await asyncio.sleep(1)
    
    # Otherwise... continue with the second rotation
    if time_rot_2 < 0:
        rc.rotate_right(speed_rot_2)
    else:
        rc.rotate_left(speed_rot_2)
    await asyncio.sleep(abs(time_rot_2))
    rc.active_stop()

"execute_safe_trajectory" moves the car at a given PWM for a given duration, unless it sees an obstacle, in which case obstacle avoidance takes over and then the function returns.

There are 1 second pauses between movements to kill momentum and make movements more stable.

Localization:

At first, we tried doing localization with only the update step as in lab 12. However, I quickly became frustrated with the robot's willingness to believe itself in a totally different corner of the map after a small inaccuracy in its observation loop or when localizing in an indistinctive grid cell. I decided that, even with a highly imperfect odometry or motion model, it would be beneficial to provide a loose prediction step to give the robot a hint to its general location before it runs the observation loop. Thus, I implemented a loose prediction step using the assumption that the robot just successfully moved from one waypoint to the next. This is clearly not a reliable assumption, but by giving the robot waypoints as a prediction I get a bel_bar matrix which is biased towards areas the robot could possibly be if the trajectory hasn't already completely failed, and the update step can then be used to localize for the actual pose of the car.

Code for Localization:

    # Prediction Step
    current_odom = waypoints[i]
    prev_odom = waypoints[0] if i == 0 else waypoints[i - 1]
    loc.prediction_step(current_odom, prev_odom)
    
    # Get Observation Data by executing a 360 degree rotation motion
    loc.get_observation_data()

    # Run Update Step
    loc.update_step()
    loc.plot_update_step_data(plot_data=True)
    argmax_bel = get_max(loc.bel)
    current_belief = loc.mapper.from_map(*argmax_bel[0])

"waypoints" is an array of poses (in grid cell indexes) starting at (-2ft, -1ft, -180deg), with waypoints[i] representing the next waypoint destination for the robot. The angle in each pose was manually assigned.

"loc.prediction_step" creates a bel_bar matrix based on a move from one pose to another as in lab 11.

"loc.update_step" runs an observation loop collecting 18 distance measurements and comparing them to pre-cached values with a Bayes Filter, as in labs 11 and 12.

Control:

To move the robot we used an open loop motor scaling function to convert distances and angles to motor inputs. I started with controlling duration as a linear function of time. This worked well for turning, but not for translation because the car did not move linearly at a constant pace, but rather accelerated continuously as motor input was applied due to Newton's second law. This made longer inputs lead to greater speeds and thus proportionally farther distances. To deal with this, I used a square root scaling function, which approximated a second derivative on the quadratic duration-to-time relationship. This proved far more effective and lead to reasonable translations for both long and short distances.

Result:

Video of run with localization plot in corner:

This run has some problems with localization from the start, but manages to recover due to some informative update step observations near the center of the map. However, as the robot attempts to move to the third and fourth waypoints, localization falls off again and it falls down a rabbit hole of inaccurate control. Still, it managed to successfully localize several times and navigate through at least two waypoints, so it was a partial success.

Conclusion:

My implementation of this lab included modified successes in control and localization, with the robot showing definite promise in its navigation. However, it could have been much improved through better control systems and more fine-tuned localization.

Note: